На привычных картах мир показан так, как его изобразил фламандский географ Герард Меркатор еще в XVI веке. Тогда он совершил революцию в картографии, но его проекция искажает реальные размеры стран. Все 2D-карты, которые существуют сегодня, неточные. Ученые решили сделать правильные плоские карты, однако они не похожи на то, что приходилось видеть ранее. Рассказываем о столетних попытках сделать правильные карты и показываем, сколько на самом деле места занимает Россия на земном шаре.
Как показать круглую Землю?
Как выровнять сферу? На протяжении веков картографы пытались точно отобразить круглую планету на плоскости. Необходимо было создать карту, которую можно положить в карман и отправляться покорять новые территории, прорисовывать маршруты и вообще увидеть всю территорию Земли одновременно.
Попыток было много.
На привычных картах мир показан так, как его изобразил фламандский географ Герард Меркатор еще в XVI веке. Тогда он совершил революцию в картографии, но его проекция искажала реальные размеры стран (линии долготы расположены параллельно друг другу, хотя в реальности они пересекаются на полюсах, — в результате объекты у полюсов оказываются намного больше по размеру, чем те, что у экватора).
Однако невозможно сделать все идеально. Карта, на которой хорошо получается одно, может не подходить для изображения другого. Популярная проекция Меркатора, которая висит на всех стенах классных комнат и используемая в качестве основы для карт Google, превосходно отображает локальные формы, но она так сильно искажает участки поверхности вблизи Северного и Южного полюсов, что полярные регионы обычно просто обрезаются.
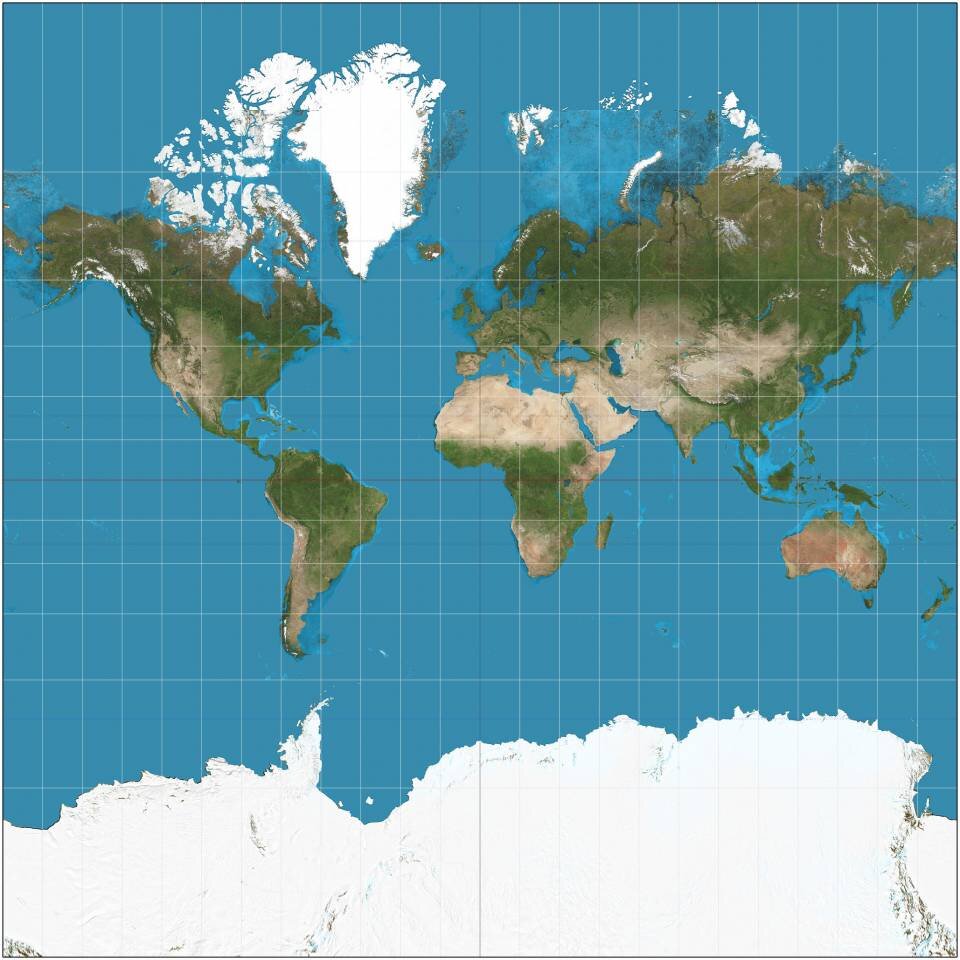
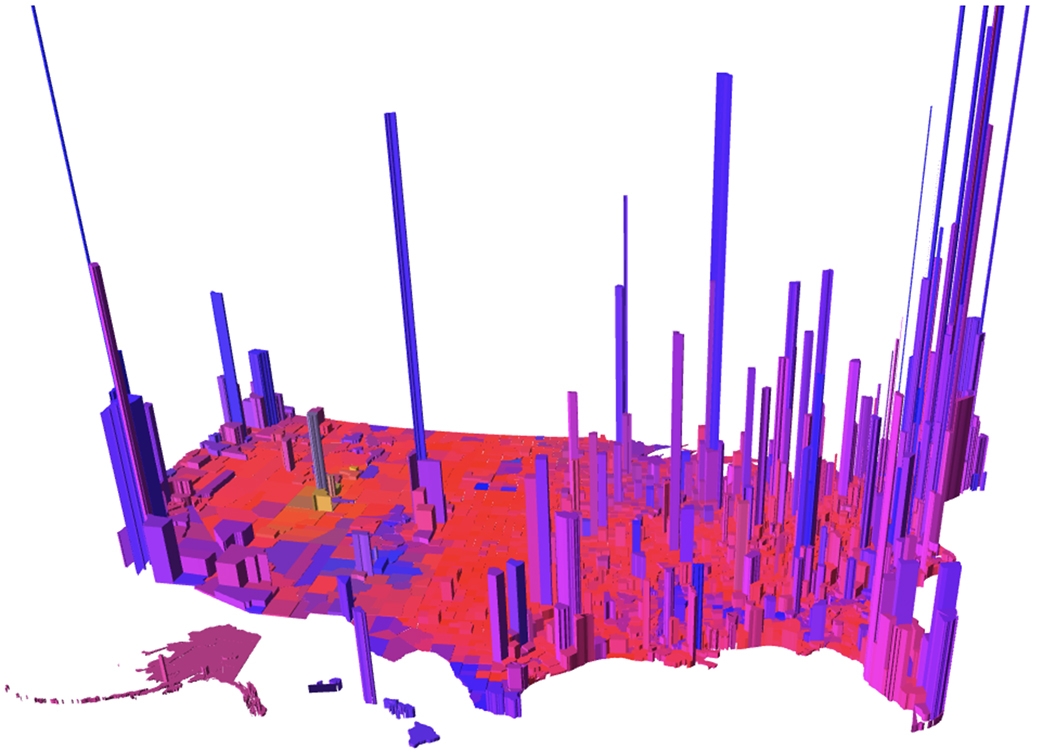
На карте True Size можно оценить это искажение: нужно выбрать любую страну, передвинуть ее на другой континент и сравнить масштабы. Например, на классической карте Россия выглядит в разы больше Африки, но в реальности она занимает только половину континента.
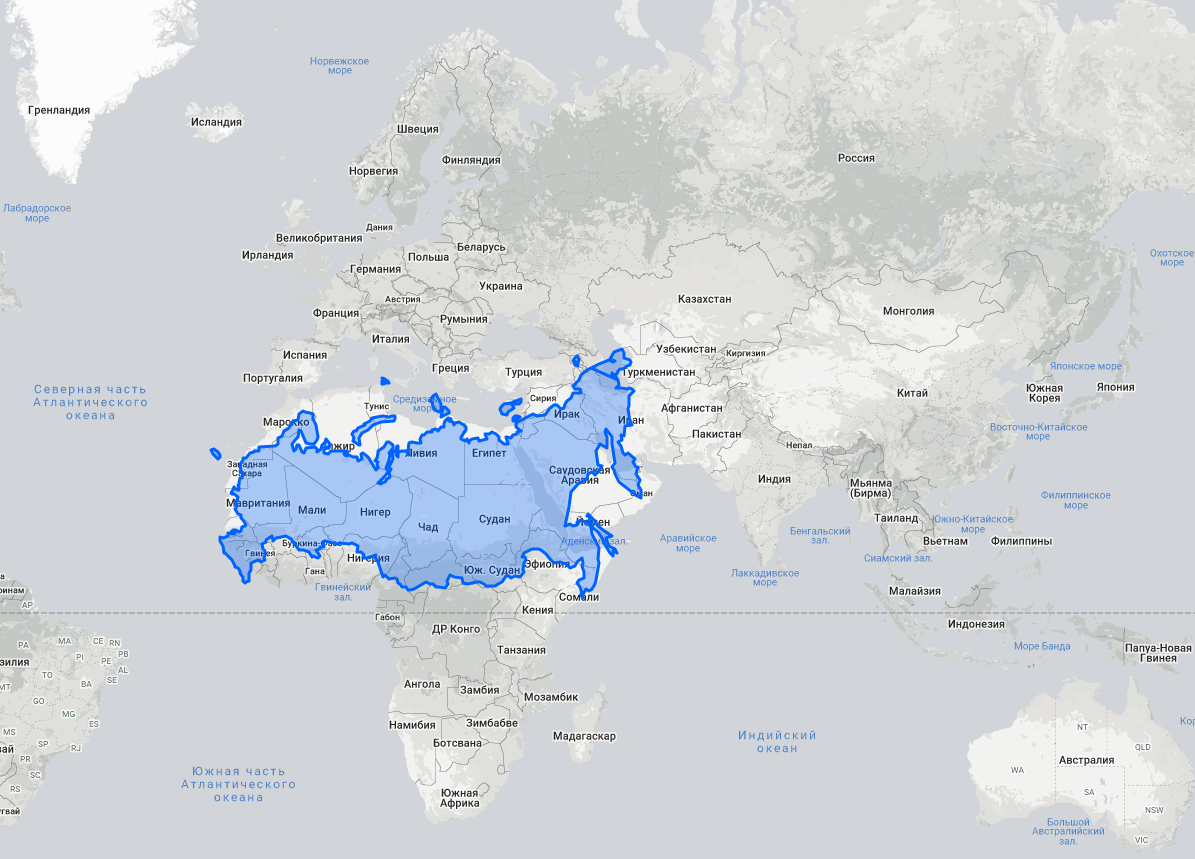
То же самое с Гренландией, которая, кажется, в два раза больше Австралии, — на деле же она занимает только треть ее площади. Китай, в свою очередь, занимает гораздо больше площади, чем кажется.
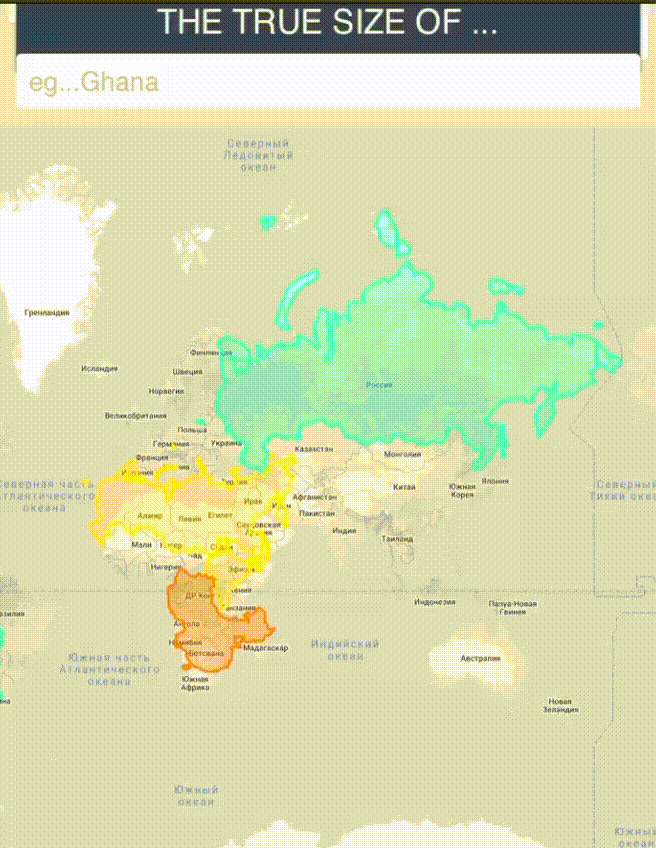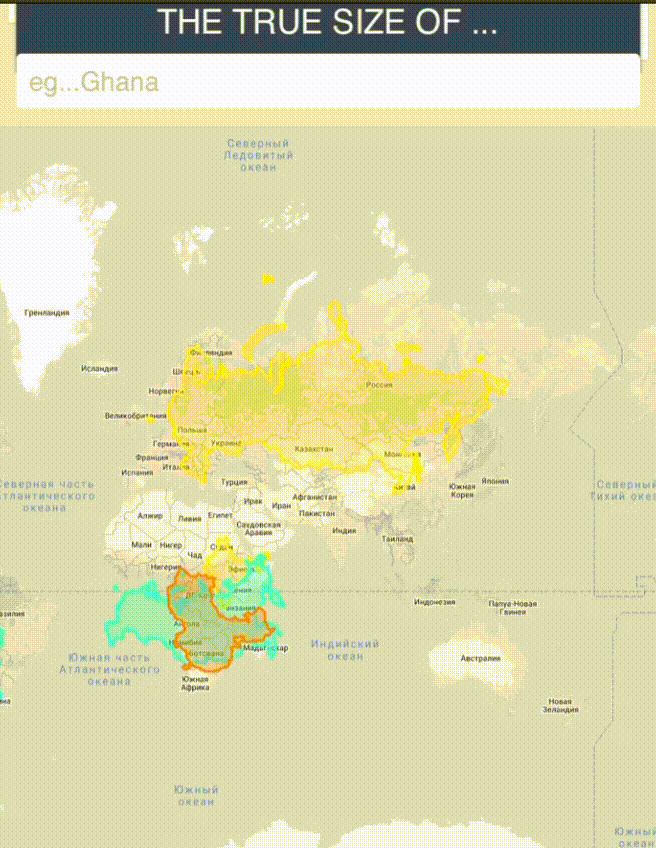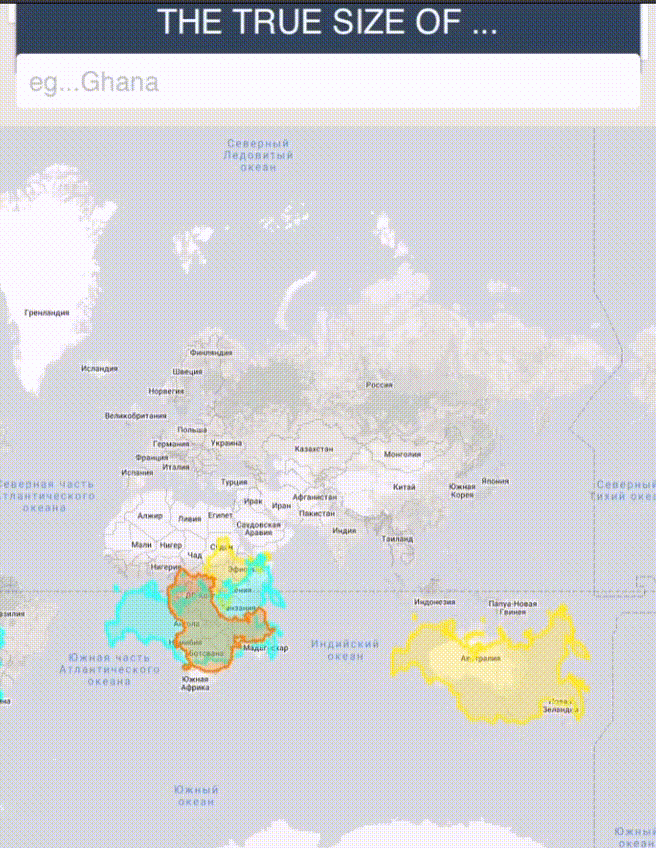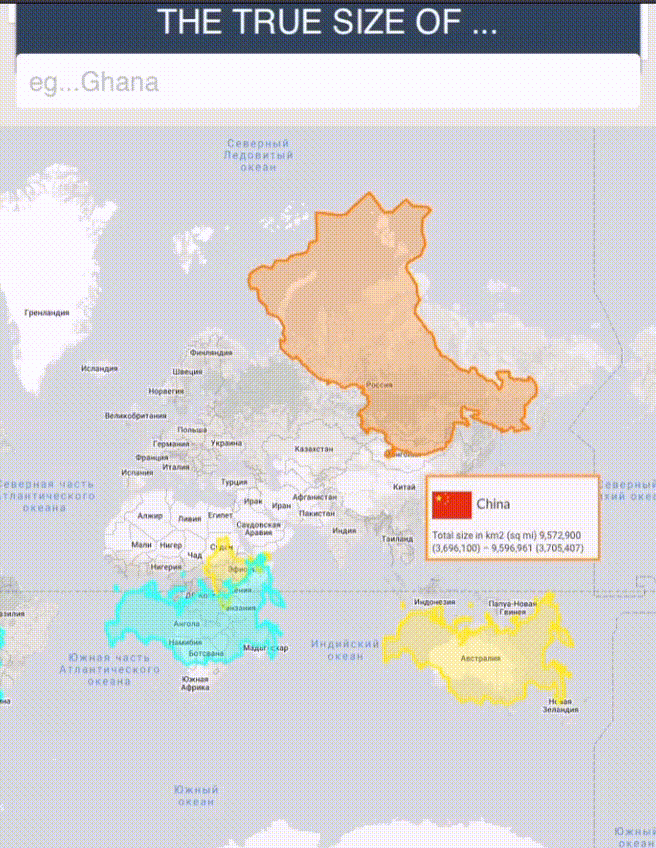
Попытки адаптации
Конечно, после создания проекции Меркатора ученые пытались сделать как можно более правдоподобную адаптацию. Как определить идеальную? В 2007 году была создана система для оценки существующих карт. Она количественно оценивает шесть типов искажений, которые вносят плоские карты: локальные формы, площади, расстояния, изгиб, асимметрия и граничные разрезы (разрывы непрерывности). Чем ниже оценка, тем лучше: у глобуса, например, оценка равна 0,0. Авторы системы — Дж. Ричард Готтом, заслуженный профессор астрофизики в Принстоне и создатель логарифмической карты Вселенной и Дэвид Голдберг, профессор физики в университете Дрекселя.
В 1921 году немецким картографом Освальдом Винкелем (Oswald Winkel) предложена модифицированная азимутальная проекция карты мира — проекция Винкеля lll (Winkel tripel projection). Это самая известная из ранее предложенных плоских картографических проекций. Название tripel (по-немецки «тройной») относится к цели Винкеля минимизировать три вида искажений: площадь, направление и расстояние.
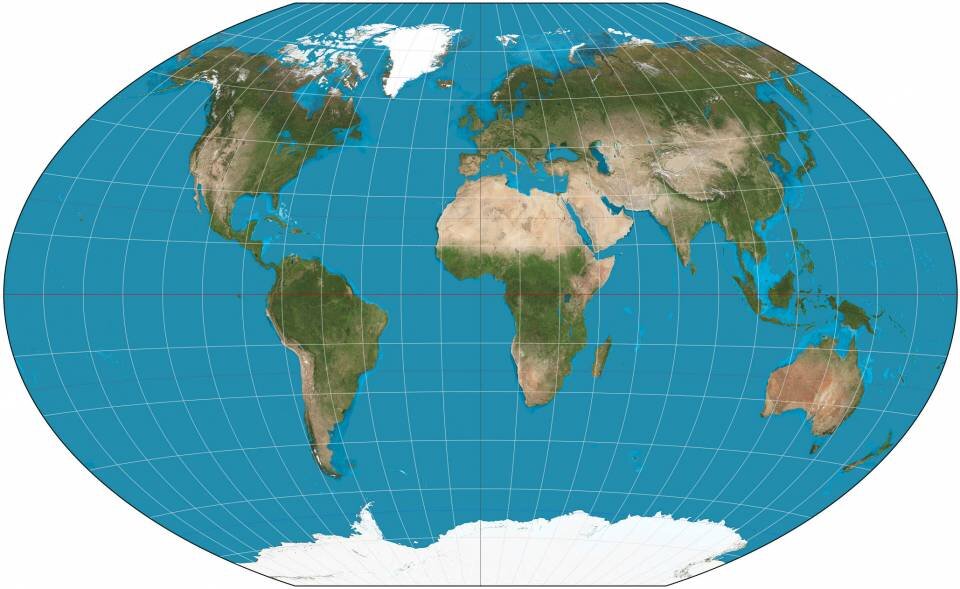
Ее оценка по системе Голдберга-Готта равна 4,563. Уже близко к нулю, однако еще оставалась проблема «пересечения границ» — разделение Тихого океана и создание иллюзии большого расстояния между Азией и Гавайями.
Попытки продолжались.
В 1943 году Бакминстер Фуллер попытался сделать карту, которая достоверно бы передавала размеры континентов. Он разбил круглую Землю на правильные формы и дал инструкции, как сложить и собрать земной шар в виде многогранного глобуса. Хотя таким образом Фуллер защитил формы континентов, он измельчил океаны, а многие между материками увеличились, например, между Австралией и Антарктидой.
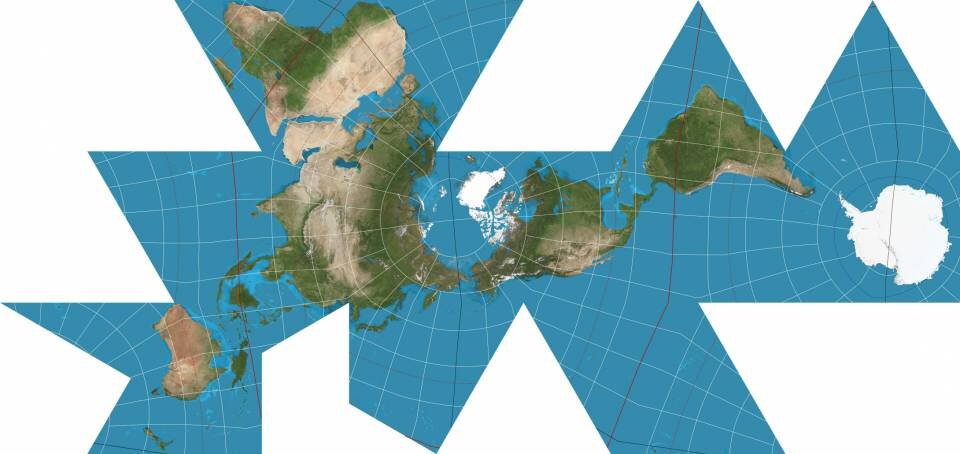
Ясно, что нужен совершенно новый подход.
Новый подход
Фундаментальное переосмысление того, как могут работать карты, привело к созданию самой точной плоской карты из когда-либо созданных. В проекте принимали участие три эксперта: Дж. Ричард Готтом, Дэвид Голдберг и Роберт Вандербей, профессор операционных исследований и финансового инжиниринга, создавший карту результатов выборов «Пурпурная Америка».
Ученые вдохновились работой Готта о многогранниках — многогранных твердых фигурах. В недавней статье он начал рассматривать новый вид многогранников с правильными формами, что привело к революционной идее двусторонней карты.
Рассказывая о новой плоской карте профессор вспомнил историю с олимпийскими прыгунами в высоту. В 1968 году Дик Фосбери шокировал спортивных фанатов, выгнув спину и перепрыгнув через перекладину назад. Он установил новый рекорд и выиграл золотую медаль, и с тех пор прыгуны в высоту поменяли тактику.
«Мы как мистер Фосбери, — объясняет Готт. — Мы делаем это, чтобы побить рекорд, сделать плоскую карту с наименьшими возможными ошибками. Так что, как и он, мы удивляем людей, предлагаем кардинально другой вид карты. Каждая из ошибок Винкеля Трипеля была учтена».
Новая карта не похожа ни на одну из предыдущих.
Решение найдено
Плоская карта, которую создали ученые, двусторонняя и круглая, как граммофонная или виниловая пластинка. Она выходит за рамки двух измерений, не теряя при этом удобства логистики — хранения и изготовления — плоской карты.
У новой двусторонней карты меньше ошибок в расстояниях, чем у любой односторонней плоской карты. Предыдущим рекордсменом была карта 2007 года, созданная Готтом с Чарльзом Муньоло, выпускником Принстона в 2005 году.
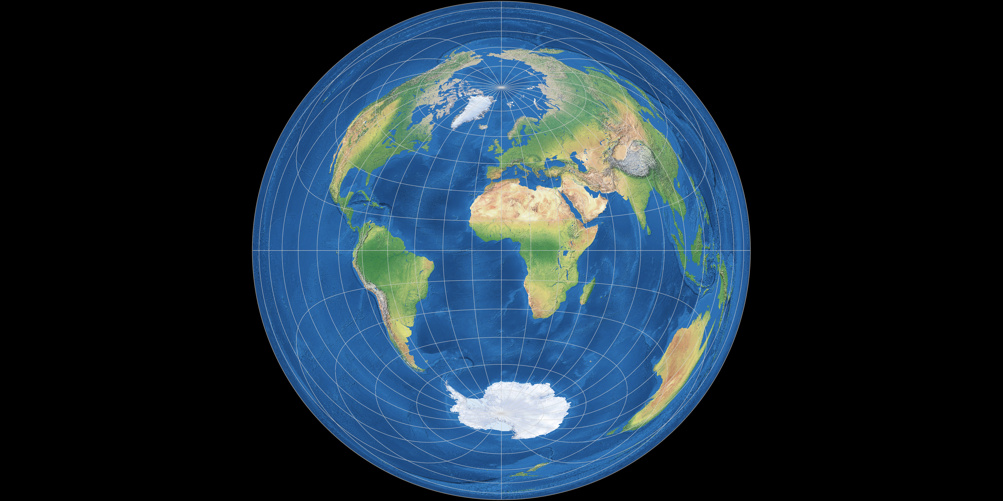
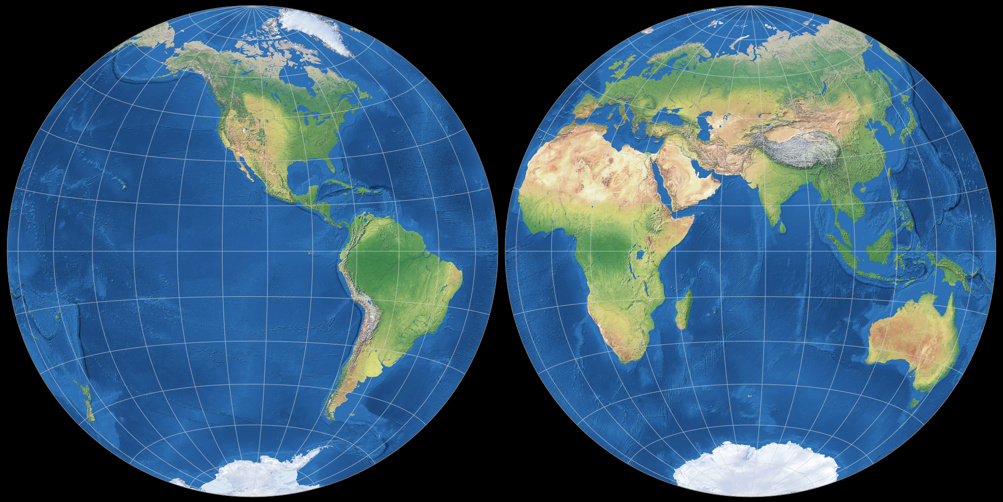
Фактически эта карта примечательна тем, что имеет верхнюю границу ошибок расстояния: отклонение расстояний более чем на ± 22,2% невозможно. Для сравнения, в проекциях Меркатора и Винкеля Трипеля, а также в других, ошибки расстояния становятся огромными по мере приближения к полюсам и по существу бесконечными от левого к правому краю (которые находятся далеко друг от друга на карте, но непосредственно примыкают к земному шару). Кроме того, площади на краю всего в 1,57 раза больше, чем в центре.
Карту можно распечатать спереди и сзади на одной странице журнала, чтобы читатель мог вырезать ее.
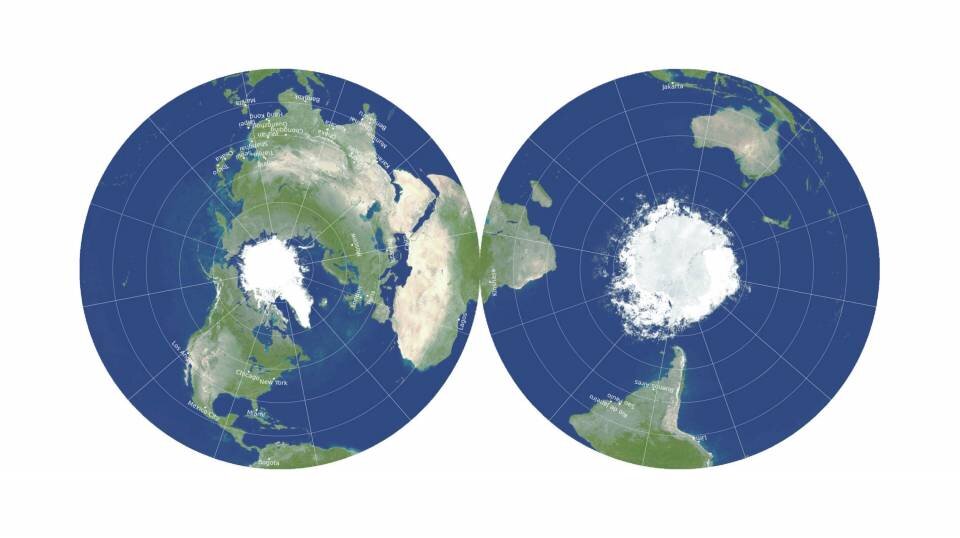
Насколько известно ученым, никто никогда раньше не делал двусторонние карты такой точности.
Leave a Reply